Introduction of Data Structures and Algorithms

Testing

All the data structures and algorithms have been tested using a minimised test
driven development style on paper to °esh out the pseudocode algorithm. We
then transcribe these tests into unit tests satisfying them one by one. When
all the test cases have been progressively satis¯ed we consider that algorithm
suitably tested.
For the most part algorithms have fairly obvious cases which need to be
satis¯ed. Some however have many areas which can prove to be more complex
to satisfy. With such algorithms we will point out the test cases which are tricky
and the corresponding portions of pseudocode within the algorithm that satisfy
that respective case.
As you become more familiar with the actual problem you will be able to
intuitively identify areas which may cause problems for your algorithms imple-
mentation. This in some cases will yield an overwhelming list of concerns which
will hinder your ability to design an algorithm greatly. When you are bom-
barded with such a vast amount of concerns look at the overall problem again
and sub-divide the problem into smaller problems. Solving the smaller problems
and then composing them is a far easier task than clouding your mind with too
many little details.
The only type of testing that we use in the implementation of all that is
provided in this book are unit tests. Because unit tests contribute such a core
piece of creating somewhat more stable software we invite the reader to view
Appendix D which describes testing in more depth.

In This topic we study about some New topic for DSA

1st we study Data Structures and Algorithms – Big Oh notation

For run time complexity analysis we use big Oh notation extensively so it is vital that you are familiar with the general concepts to determine which is the best algorithm for you in certain scenarios. We have chosen to use big Oh notation for a few reasons, the most important of which is that it provides an abstract measurement by which we can judge the performance of algorithms without using mathematical proofs.

2nd we study Data Structures and Algorithms – Imperative programming language

In The last lecture we study about – Big Oh notation
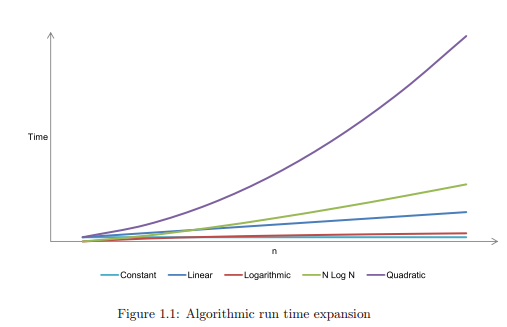
Figure 1.1 shows some of the run times to demonstrate how important it is to choose an efficient algorithm. For the sanity of our graph we have omitted cubic O(n 3 ), and exponential O(2n) run times. Cubic and exponential algorithms should only ever be used for very small problems (if ever!); avoid them if feasibly possible.
The following list explains some of the most common big Oh notations:
O(1) constant: the operation doesn’t depend on the size of its input, e.g. adding a node to the tail of a linked list where we always maintain a pointer to the tail node.
O(n) linear: the run time complexity is proportionate to the size of n.

3rd we study about Introduction of Data Structures and Algorithms – Object oriented concepts, Pseudo code

Object oriented concepts
For the most part this book does not use features that are speci¯c to any one
language. In particular, we never provide data structures or algorithms that
work on generic types|this is in order to make the samples as easy to follow
as possible. However, to appreciate the designs of our data structures you will
need to be familiar with the following object oriented (OO) concepts

And we will study in the next topic for DSA
Linked Lists