
If the water changes to gas then this is called volatility. Similarly, if data has random stages such as Brownian motion than this also means that data is volatile.
The variation in data is mostly due to internal factors. The external factor does not change the volatility or does not bring volatility, but it may work as a catalyst to expose the data.
ARCH models & generalized autoregressive conditional heteroskedasticity can be best explain by below model:
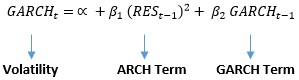
Volatility= ∝ + ARCH Term+ GARCH Term
Volatility is gauged by the model known as GARCH and the econometrical tool used is known as ARCH.
ARCH models & generalized autoregressive conditional heteroskedasticity model can be mathematically be expressed as:
Whereas, GARCH is also known as volatility.
To understand ARCH models & generalized autoregressive conditional heteroskedasticity, you first need to understand the concept of Heteroskedasticity and Homoscedasticity.
Consider below model:
X= ∝ + β Y+ET
Suppose for the above model, we have different values of x and y with respect to the change in years, whereas ET remains same as mention in below table:
Considering the above model and the table we can now define Homo / Heteroskedasticity as:
When independent variable explains or predicts the dependent variable and at every time “ET” or error term remains same, then this is called homoskedasticity, where as if “ET” is different as shown in below table, then this is called heteroskedasticity.
The formula for the moment is: Moment= (∑(x-AM)^n )/N
Where, AM = Arithmetic mean, N = total number of observation, n = nth Moment about mean
If n = 2, then this equation turns to Variance.
Therefore the mathematical expression or the formula for Homo / Heteroskedasticity can be further derived from the variance formula as mentioned below:
Where ET = Error term and AM (ET) = Arithmetic mean of the error term.
If H = 0, then this means homoskedasticity is present, else Heteroskedasticity.
The term ARCH stands for Auto Regressive conditional heteroskedasticity. Up till now we are clear on all of the terms meaning in ARCH except for conditional heteroskedasticity. If heteroskedasticity is due to any condition that is due to any catalyst involved then this kind of heteroskedasticity will be termed as conditional heteroskedasticity. Therefore we can summarize, that if AR process exists in a model and side by side heteroskedasticity exists due to any catalyst present then this will be known as ARCH.
Remember: if homoskedacity is present then volatility cannot exist, whereas on the other hand if heteroskedasticity is there, then volatility may exist.
What is the Main Cause of a Heart Attack? What is its Solution? A heart attack is the blockage of… Read More
In the vast economic arena, one term that often takes center stage, inciting extensive debates and discussions, is the "debt… Read More
De-Dollarization: The Changing Face of Global Finance The financial landscape is in a state of flux, with an intriguing economic… Read More
The curtains closed on a dramatic Bundesliga season with Bayern Munich standing tall once again, clinching their 11th straight title.… Read More
The Unfolding Story of Celine Dion's Health In recent news that has left fans across the globe stunned, iconic singer… Read More
As the echoes of the recent NBA season start to fade, the attention of enthusiasts is firmly glued to one… Read More